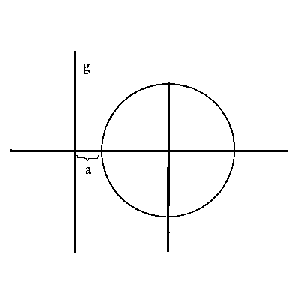Mein Gehirn ist in keinem günstigen Zustand. Es war immer seine Haupteigenschaft ein Mangel an Extensität & eine ziemlich große Intensität. Nun läßt die Intensität nach und wird nicht durch etwas anderes kompensiert. Ich schreibe nicht alles ein es scheint mir unrecht alles breitzutreten wenn ich es nicht bessern kann oder will.
Alles was ich jetzt in der Philosophie hinschreibe ist mehr oder weniger fades Zeug. Ich halte es aber für möglich daß es besser wird.

Ich habe sehr genußreiche Diskussionen mit Ramsey über Logik etc. Sie haben etwas von einem kräftigen Sport & sind glaube ich in einem guten Geist geführt. Es ist etwas Erotisches & Ritterliches darin. Ich werde dabei auch zu einem gewissen Mut im Denken erzogen. Es kann mir beinahe nichts Angenehmeres geschehen als wenn mir jemand meine Gedanken gleichsam aus dem Mund nimmt & sie gleichsam im Freien aufrollt. Natürlich ist alles das mit viel Eitelkeit gemischt, aber es ist nicht pure Eitelkeit.

Ich gehe in der Wissenschaft nur gern allein spazieren.

Ist ein Raum denkbar der nur alle rationalen aber nicht die irrationalen Punkte enthält?
Und das heißt nur: Sind die irrationalen Zahlen nicht in den rationalen bereits präjudiziert?

Kann ich den Raum in rationalen Zahlen abbilden so kann ich ihn auch in irrationalen Zahlen abbilden. Und ist die eine Abbildung gegeben so ist damit auch schon die andere Art der Abbildung gegeben.

Nun frägt es sich: Gibt es eine bevorzugte, etwa besonders unmittelbare, Art der Abbildung? Ich glaube nein!

Jede Art der Abbildung ist gleichberechtigt.

Wie läßt sich aber eine Entscheidung darüber denken welcher Art die Kontinuität des Gesichtsraumes ist?

Aber man kann sagen: Die Physik hat eine Sprache & in dieser Sprache sagt sie Sätze. Diese Sätze können wahr oder falsch sein. Diese Sätze bilden die Physik & ihre Grammatik die Phänomenologie (oder wie man es nennen will).

Die Sache schaut aber in Wirklichkeit schwieriger aus durch den Gebrauch der mathematischen Terminologie. Wenn z.B. die Wissenschaft zweifelt ob die beobachteten Erscheinungen durch die Elektronen- oder durch die Quantentheorie richtig zu beschreiben sind, so scheint es auf

Es gibt eine bestimmte Mannigfaltigkeit des Sinnes & eine andere Mannigfaltigkeit der Gesetze.

Die Physik unterscheidet sich von der Phänomenologie dadurch daß sie Gesetze feststellen will. Die Phänomenologie stellt nur die Möglichkeiten fest.

Dann wäre also die Phänomenologie die Grammatik der Beschreibung derjenigen Tatsachen, auf denen die Physik ihre Theorien aufbaut.

Erklären ist mehr als beschreiben. Aber jede Erklärung enthält eine Beschreibung.

Kann man denn das Gesichtsfeld oder einen Teil des Gesichtsfeldes überhaupt beschreiben?

Man kann gewiß sagen: Wenn Du in dieses

Irgendwie scheint es mir als wäre jeder einfärbige Fleck im Gesichtsfeld einfach & als wäre seine Zusammengesetztheit aus kleineren Teilen nur eine scheinbare.

Man könnte glauben der Gesichtsraum sei aus minima visibilia zusammengesetzt etwa aus lauter kleinen Quadraten die man als unteilbare Flecke sieht. Aber dann ist die Wahl dieser Flecke || Teile offenbar willkürlich. Ich könnte z.B. nicht sagen wie das Quadratnetz über ein bestimmtes Bild zu legen ist denn wenn man das Netz um weniger als eine Maschenweite verschiebt so sind die minima visibilia zwar in ganz anderen Orten aber das Bild sieht ganz gleich aus.

Es scheint als könne man einen einfärbigen Fleck nicht zusammengesetzt sehen außer wenn man ihn sich nicht einfärbig

Das würde heißen: Die einfachen Bestandteile des Gesichtsfeldes sind einfärbige Flecke.
     Wie verhält es sich aber dann mit kontinuierlichen Farbenübergängen?

Wie kann man die Form eines || Gestalt eines Flecks im Gesichtsfeld beschreiben?

Kann man im Gesichtsfeld Koordinatengeometrie treiben?

Kann man sagen daß der kleinere Fleck einfacher ist als der größere?
     Nehmen wir an sie seien konzentrische || einfärbige Kreise, worin soll die größere Einfachheit des kleineren Kreises bestehen?

Man könnte sagen der größere kann zwar aus dem kleineren & noch einem Teil bestehen aber nicht vice versa. Aber warum soll

Es scheint mir also: Der größere || kleinere Fleck ist nicht einfacher als der größere.

Was ist die allgemeine Form der räumlichen Aussagen?

Es scheint mir eine eigentümliche Eigenschaft der räumlichen Aussagen daß man scheinbar den Raum ohne irgend eine Anspielung auf die Zeit nicht beschreiben kann. Ich kann z.B. sagen: „Ich sehe jetzt zwei rote Kreise || einen roten Kreis auf blauem Grund”. Das ist ein Satz. Aber ich kann nicht sagen „ein roter Kreis ist auf blauem Grund”.

Es ist eigentlich von vornherein wahrscheinlich daß die Zeit in die Betrachtung des Gesichtsraumes nicht nachträglich als ein Anhängsel eintreten kann.

Es ist doch sehr seltsam daß man immer

Ein Gegenstand darf sich in gewissem Sinne nicht beschreiben lassen.

D.h. die Beschreibung darf ihm keine Eigenschaften zuschreiben deren Fehlen die Existenz des Gegenstandes selbst vernichten || zunichte machen würde. D.h. die Beschreibung darf nichts aussagen was für die Existenz des Gegenstandes wesentlich wäre.

„Der Mord … beschäftigt das Gericht” ist ein Satz in dem offenbar ein Ereignis mit scheinbar mit einem Namen bezeichnet ist. Es ist das nicht vielleicht ein Fall der Russellschen „Descriptions” sondern der Fall in dem scheinbar von einem komplexen Gegenstand die Rede ist der aber bei richtiger Analyse durch einen Satz (die Beschreibung des Komplexes) dargestellt wird.

Es wäre vielleicht nützlich erst über die Darstellung irgend eines Raumes nachzudenken ehe man zum Gesichtsraum übergeht.

Die Frage ist dann etwa: Wie muß man ein System von Axiomen richtig interpretieren damit es zur Darstellung einer Variablen wird?

Verhält es sich so daß die „Axiome” in einer gewissen Struktur Tautologien sind & daß diese Struktur eben dadurch bestimmt wird daß gewisse Sätze in ihr Tautologien werden?

Man könnte gewiß statt der Logik

Alle Gleichungen – || , nicht nur die Definitionen – || , sind Zeichenregeln.
     Von einigen dieser Zeichenregeln kann man zu den anderen gelangen. Man kann die einen geben & aus ihnen die anderen ableiten.

Ist so eine Ableitung ein Schlußverfahren? Warum soll man es nicht so nennen?

Wie verhält es sich mit Ungleichungen? Auch sie sind offenbar Zeichenregeln.
     Kann man Zeichenregeln durch Sätze – die von den Zeichen handeln – ersetzen?
     Wenn ja, so ist es klar daß ich die ganze Logik auf Zeichenregeln, also

Ich werde scheinbar, wider meinen Willen, auf die Arithmetik zurückgeworfen.

Die Zahl ist eine Art der Darstellung. Wenn ich sage: auf dem Tisch liegen 4 Bücher so könnte ich dasselbe auch ohne die Hilfe der Zahl 4 ausdrücken etwa mit Hilfe einer anderen Zahl. Die 4 kommt in meine Darstellung dadurch daß ich sie in Form eines Satzes über a, b, c, d ausdrücke.

Ein Satz handelt von 4 Dingen wenn er von a, b, c, d handelt.

Das charakteristische ist daß das was man zählt durch Substantive bezeichnet wird.

Man müßte also den Gebrauch der Substantive in der Sprache allgemein rechtfertigen.

     Kann das geschehen indem man Substantive

Stelle ich eine Tatsache durch einen Satz von der Form φ(A,B) dar so sagen wir || könnten wir sagen die Darstellung enthält eine Zweiheit u.s.w.

Wie verhält sich diese Theorie zu der Freges & Russells? Der erste Unterschied ist, daß in der Theorie Freges eine Einseinsrelation konstruiert wird das ist unerlaubt & setzt eine falsche Auffassung der Identität voraus. Zweitens wird eine Klasse mit einer bestimmten Anzahl von Gliedern konstruiert & das ist aus dem gleichen Grund unerlaubt. Diese Grundklasse ist || wäre in meiner Theorie die Klasse der Substantiva in einem gewissen

Anderseits scheint es als könne man meine Theorie auch so formulieren daß, wie Frege es sagt, die Zahlangabe eine Aussage über einen Begriff ist.

Ich sagte einmal es gäbe keine extensionale Unendlichkeit. Ramsey sagt darauf kann man sich nicht vorstellen daß ein Mensch ewig lebt d.h. einfach nie stirbt, und ist das nicht extensionale Unendlichkeit? Ich kann mir doch gewiß denken daß ein Rad sich dreht und nie stehenbleibt. Hier liegt eine merkwürdige Schwierigkeit: Es scheint mir unsinnig zu sagen daß in einem Raum unendlich viele Gegenstände || Körper sind gleichsam als etwas Zufälliges. Dagegen kann ich mir ja intentional ein unendliches Gesetz denken (oder eine unendliche Regel) durch die immer neues produziert wird – ad infinitum – aber natürlich nur was eine Regel produzieren kann, nämlich Konstruktionen.
     Und nun scheint es daß die unendlichen

Angenommen wir wandern auf einer Geraden in den Euklidischen Raum hinaus & sagen wir begegnen alle 10 m einer eisernen Kugel von gewissem Durchmesser ad inf.; ist das eine Konstruktion? Es scheint ja. Das merkwürdige ist daß man einen solchen unendlichen Komplex von Kugeln auffassen kann als das unendliche || endlose Wiederkehren derselben Kugel nach einem gewissen Gesetz. Daß aber im selben Augenblick wenn man eine individuelle Verschiedenheit der Kugeln denkt die || ihre unendliche Anzahl Unsinn zu werden scheint.

Ich habe das Gefühl daß die bloß negative Beschreibung des nicht Aufhörens nicht eine positive Unendlichkeit liefern kann.

Das || Dieses negative Kennzeichen genügt wohl

Wenn zwei Gegenstände alle Eigenschaften mit einander gemein haben, wie können sie dann verschiedene Namen haben? Denn daß sie Namen haben ist ja in diesem Sinne auch eine Eigenschaft!

Nun kann ich aber doch über die Eigenschaften der Gegenstände unsicher sein. Ich kann also zweifeln ob zwei Gegenstände alle Eigenschaften miteinander gemein haben oder nicht. Wie geht es weiter? Ich würde ihnen etwa zuerst verschiedene Namen geben …?
     Nein denn sobald || wenn ich ihnen auch nur verschiedene Namen geben kann so haben sie damit eo ipso verschiedene Eigenschaften. Das würde aber heißen daß ich von zwei Gegenständen gar nicht sagen kann daß sie nur gleiche Eigenschaften haben, denn dieser Satz würde sich selbst widersprechen.

Angenommen mein Gesichtsbild besteht aus zwei gleichgroßen roten Kreisen auf blauem Grund: Was ist hier in zweifacher Zahl vorhanden & was einmal? Und was heißt || bedeutet diese Frage überhaupt?

Man könnte sagen wir haben hier eine Farbe, eine Form aber zwei Örtlichkeiten. Aber kann man denn von Örtlichkeiten reden ohne sie sich erfüllt zu denken also als bloße Möglichkeiten?
     Ein scheinbarer Ausweg wäre natürlich der, zu sagen, rot, kreisförmig, sind Eigenschaften (externe) von zwei Gegenständen die man etwa Flecken nennen könnte & diese Flecken stehen außerdem in gewissen räumlichen Beziehungen zu einander; aber das ist Unsinn.

Es ist offenbar möglich die Identität eines Ortes im Gesichtsfeld festzustellen denn sonst könnte man nicht unterscheiden

Man kann auch sagen der Gesichtsraum ist ein gerichteter Raum, ein Raum in dem es ein oben & unten und ein rechts & links gibt. Und dieses oben & unten, & rechts & links hat nichts mit der Schwerkraft oder der rechten & linken Hand zu tun. Es würde z.B. auch dann seinen Sinn beibehalten wenn wir unser ganzes Leben lang durch ein Teleskop nach den

Angenommen wir sähen durch ein Fernrohr nach dem Sternenhimmel dann wäre unser Gesichtsfeld gänzlich dunkel mit einem helleren Kreis & in diesem Kreis wären Lichtpunkte. Nehmen wir ferner an wir hätten unseren Körper nie gesehen sondern immer nur dieses Bild wir könnten also nicht die Lage eines Sterns mit der unseres Kopfes oder unserer Füße vergleichen. Was zeigt mir dann daß mein Raum ein oben & unten etc. hat, oder einfach, daß er gerichtet ist? Ich kann jedenfalls wahrnehmen daß sich das ganze Sternbild im lichten Kreis dreht & das heißt ich kann verschiedene Richtungen des Sternbilds wahrnehmen. Wenn ich z.B. ein Buch verkehrt halte so kann ich die Buchstaben nicht oder doch schwer lesen.

Dieser Sachverhalt ist nicht vielleicht damit || dadurch erklärt daß man sagt: Die Retina hat eben ein oben & unten, rechts & links & so ist es leicht verständlich daß es das

Wir können auch sagen es verhält sich in unserem Gesichtsfeld immer als sähen wir mit allem übrigen ein gerichtetes Koordinatensystem wonach wir alle Richtungen fixieren können. – Aber auch das ist keine richtige Darstellung denn sähen wir wirklich ein solches Koordinatenkreuz (etwa mit Pfeilen) so wären wir tatsächlich im Stande nicht nur die relativen Richtungen der Objekte gegen dieses Kreuz zu fixieren sondern auch die Lage des Kreuzes selbst im Raum gleichsam gegen ein ungesehenes im Wesen dieses Raumes enthaltenes Koordinatensystem.

Wie müßte es sich mit unserem Gesichtsfeld verhalten wenn das nicht so wäre? Ich könnte dann natürlich relative Lagen & Lageänderungen sehen aber nicht absolute. D.h. aber z.B. es hätte keinen Sinn von einer

Wir könnten das auch so darstellen: Nehmen wir an daß einmal für ein paar Augenblicke ein gerichtetes Koordinatenkreuz in unserm Gesichtsfeld aufgeflammt sei & dann wieder verschwunden so könnten wir bei genügendem Gedächtnis die Richtung jedes später eintretenden Bildes nach der Erinnerung an das Kreuz fixieren. Gäbe es keine absolute Richtung so

Das heißt aber wir haben die Möglichkeit eine mögliche Lage – d.h. also eine Stelle – im Gesichtsfeld zu beschreiben ohne daß auf etwas hingewiesen wird || auf etwas hinzuweisen || uns auf etwas zu beziehen was sich eben dort befindet. Wir können also z.B. sagen etwas kann oben rechts sein u.s.w.
(Die Analogie mit der gekrümmten Fläche wäre etwa zu sagen: Ein Fleck auf einem Ei kann sich nahe am stumpfen Ende befinden.)

Ich kann offenbar das Zeichen V einmal als ein v einmal als ein a, einmal als das Zeichen für größer oder als das Zeichen für kleiner sehen auch wenn ich es durch ein Fernrohr sehe & meine || seine Lage nicht mit der Lage meines Körpers vergleichen kann.
     Vielleicht wird man sagen daß ich die Lage meines Körpers fühle ohne ihn zu sehen. Aber die Lage im Gefühlsraum (wie ich ihn einmal nennen will) hat mit der Lage im Gesichtsraum nichts zu tun, die beiden sind von einander unabhängig & gäbe es im

Kann ich nun etwa sagen: Die obere Hälfte meines Gesichtsfeldes ist rot.? die untere weiß.﹖ Und was bedeutet das? Kann es sagen daß ein Gegenstand (die obere Hälfte) die Eigenschaft rot hat?
     Man muß sich daran erinnern daß jeder Teil des Gesichtsraumes eine Farbe haben muß & daß jede Farbe einen Teil des Gesichtsraumes einnehmen muß. Die Formen Farbe & Gesichtsraum durchdringen einander.

Man könnte auch sagen es ist nur eine Form. Welches aber sind die Gegenstände die in dieser Form auftreten.

Stehen nicht Farbe & Gesichtsraum zu einander im Verhältnis wie Argument & Funktion? Die Formen von Argument & Funktion müssen einander auch durchdringen.

Mit der Zusammengesetztheit der räumlichen Gebilde aus ihren kleineren räumlichen Bestandteilen verhält es sich so: Das größere geometrische Gebilde ist nicht aus kleineren geometrischen Gebilden zusammengesetzt ganz ebensowenig wie man sagen kann daß 5 aus 3 & 2 zusammengesetzt ist oder etwa gar 2 aus 5 & ‒ 3. Denn hier bedingt das größere das kleinere ganz ebenso wie das kleinere das größere. Das Viereck besteht nicht aus den Vierecken … & … || ist nicht aus den Vierecken & zusammengesetzt. Vielmehr bedingt die erste geometrische Figur die beiden anderen und umgekehrt. Hier hätte also Nicod recht wenn er sagt daß die größere Figur nicht die kleineren als Bestandteile enthält. Anders aber ist es im erfüllten Raum die Figur besteht tatsächlich aus den Bestandteilen und obwohl die rein geometrische Figur des großen Vierecks || Quadrats nicht aus den Figuren der beiden Rechtecke besteht. Diese „rein geometrischen Figuren” sind ja nur logische Möglichkeiten. – Man kann nun tatsächlich ein materielles Schachbrett als Einheit – nicht aus seinen Feldern zusammengesetzt – sehen,

indem man es als ein großes Viereck sieht & von seinen Feldern absieht. – Sieht man aber von seinen Feldern nicht ab dann ist es ein Komplex & die Felder sind seine Bestandteile die es konstituieren nicht nur determinieren um die Ausdrucksweise Nicods anzuwenden.

Was es übrigens heißen soll daß etwas von irgendwelchen Gegenständen konstituiert aber nicht determiniert || determiniert aber nicht konstituiert wird kann ich nicht verstehen. Diese beiden Ausdrücke, wenn sie überhaupt einen Sinn haben, haben denselben Sinn.

Man kann die obigen Überlegungen natürlich auch auf die Zeit anwenden.

Ein Intellekt der die Bestandteile & ihre Relationen sieht || übersieht das Ganze aber nicht ist ein Unding. (siehe Nicod)

Wenn jeder Punkt im Gesichtsraum ein ausgezeichneter Punkt ist so es hat || hat es allerdings einen Sinn von hier & dort im Gesichtsraum zu sprechen & das scheint

Ist nun nicht der Begriff der Distanz einfacher zu verstehen?
     Nehmen wir ein Kraftfeld an || Denken wir uns ein Kraftfeld etwa eine Eisenplatte die in einem Punkt ständig erhitzt wird, & die Wärme nach allen Richtungen leitet so daß ein Temperaturgefälle in radialer Richtung entsteht. In allen Punkten der Fläche könne man mit Thermometern die Temperatur messen. Man könnte dann die Distanz in der Temperaturgeometrie einer || der Fläche definieren als die Temperaturdifferenz irgend zweier Thermometer.
     Auch unser Gesichtsraum wäre ja so ein Feld.

Was bedeutet dann eine Distanz im Euklidischen Raum? Aber hier bin ich, im Gegensatz zum Gesichtsraum, im Bereich der starren Maßstäbe.

Es ist nun ein Satz zu sagen: Rot ist hier. Dabei ist „hier” ein Name || die || eine || die Bezeichnung eines Ortes im Gesichtsfeld & diese Bezeichnung, bezeichnet auch die Gestalt des roten Flecks denn aus der Lage der Farbe Rot geht diese Gestalt hervor. Wie aber ist diese Lage wirklich zu beschreiben?

Der Unterschied zwischen der Geometrie als der Lehre vom || von einem Raum & der mathematischen Geometrie muß derselbe sein wie der zwischen dem Satz zwei Pflaumen & zwei Pflaumen sind vier Pflaumen & dem Satz 2 + 2 = 4. Aber auch das erste dieser Gebilde ist ja kein wirklicher Satz sondern nur eine Andeutung eines Übergangs von einem Satz zu einem anderen Satz. Daher können auch die scheinbaren Sätze der Geometrie nicht wirklich Sätze sein sondern angedeutete Übergänge von einem Satz über räumliche Objekte zu einem anderen Satz über räumliche Objekte. So kann ich von dem Satz „A & B liegen zwischen C & D” unmittelbar übergehen zu „A liegt entweder zwischen B & C oder zwischen B & D”. Das Axiom, welches mir diesen Übergang zu gestatten scheint, ist eine Tautologie, oder es ist irgendetwas anderes über seine Form bestimmt, welches es erst zu einem Kriterium für die Formen der beiden Sätze die es verbindet machen kann.

Es ist klar, daß es keine Relation des „Sich-Befindens” gibt die zwischen einer Farbe & einem Ort bestünde in dem sie „sich befindet”! Es gibt kein Zwischenglied zwischen Farbe & Raum.

Farbe & Raum sättigen einander.

Und die Art wie sie einander durchdringen macht das Gesichtsfeld.

Könnte man nicht die Axiome der Geometrie als Prinzipe des Übergangs von einem Satz zu einem anderen auffassen? Dann wären sie wirklich als Sätze der Grammatik aufgefaßt die nur solange notwendig || nötig sind als man die interne Relation zwischen den Gliedern eines Schlusses nicht aus der Struktur der Sätze ersehen kann. Sie sind dann von der Art: Man kann || darf immer von einem Zeichen das so & so aussieht zu einem anderen übergehen das so & so aussieht. (Solche Regeln des Übergangs findet man z.B. bei Frege angegeben.)

Wie verhält es sich mit der Widerspruchsfreiheit der Axiome?

Man braucht – so kommt es mir vor – um den Raum darzustellen gleichsam ein dehnbares Zeichen.
     Vielleicht ein Zeichen das eine Interpolation erlaubt analog dem Dezimalsystem.
     Das Zeichen muß die Mannigfaltigkeit & Eigenschaften des Raumes haben.

Ist nicht das Dezimalsystem mit seiner unendlichen Möglichkeit der Interpolation eben dieses Zeichen?

Die Regeln über das Zahlensystem – etwa das Dezimalsystem – enthalten alles was an den Zahlen unendlich ist. Daß diese Regeln z.B. die Zahlen nach || Zahlzeichen nach rechts & links nicht beschränken darin liegt die Unendlichkeit ausgedrückt.
     Man könnte vielleicht sagen: ja, aber die Zahlzeichen sind doch durch den Gebrauch von Papier & Schreibmaterial & andere Umstände beschränkt. Sehr wohl aber das ist nicht in den Regeln über ihren Gebrauch ausgedrückt & nur in diesen liegt ihr eigentliches Wesen ausgesprochen.

Welcher Art ist der Satz „zwischen 5 & 8 gibt es eine Primzahl”? Ich würde sagen: „das zeigt sich”. Und das ist richtig; aber kann man nicht die Aufmerksamkeit auf diesen internen Sachverhalt lenken? Man könnte doch sagen: „Untersuche das Intervall von 10 - || bis 20 auf Primzahlen! Wieviel gibt es?” Wäre das nicht eine klare Aufgabe? Und was wäre ihre Lösung? D.h., wie wäre ihre Lösung richtig auszudrücken oder darzustellen? Was bedeutet der Satz: „Zwischen 10 & 20 gibt es 4 Primzahlen”?

     Dieser Satz scheint unsere Aufmerksamkeit auf einen gewissen Aspekt der Sache zu lenken.

So kann ich z.B. die Zahl 5 so hinschreiben daß man deutlich sieht daß sie nur durch 1 & durch sich selbst teilbar ist: Etwa so:

Das käme vielleicht auf dasselbe hinaus, was ich schon früher einmal gesagt habe, nämlich, daß der eigentliche mathematische Satz ein Beweis eines sogenannten mathematischen Satzes ist. Der eigentliche mathematische Satz ist der Beweis: d.h. dasjenige was zeigt wie es sich verhält.
     Ein Beweis heißt mit Recht auch eine Demonstration.

Wenn ich jemanden frage „wieviel Primzahlen gibt es zwischen 10 & 20?”, so wird er sagen: „Ich weiß es nicht im Augenblick, aber ich kann es jederzeit feststellen”. Denn es ist ja gleichsam schon irgendwo aufgeschrieben; er muß nur nachsehen. Und wenn er nun das was er dort sieht in den Worten ausdrückt „es gibt 4 Primzahlen etc.”, müssen dann nicht die Worte ebendas spiegeln was er gesehen hat? ⁴

Man könnte das auch so sagen: der völlig analysierte mathematische Satz ist sein eigener Beweis.
     Oder auch so: der mathematische Satz ist nur die sofort sichtbare Oberfläche des ganzen Beweiskörpers der hinter der Fläche liegt. || den sie vorne begrenzt.
     Der sogenannte mathematische Satz ist – im Gegensatz zu einem eigentlichen Satz – wesentlich das letzte Glied einer Demonstration die ihn als richtig oder unrichtig sichtbar macht.

Wie kommt es dann aber, daß man doch scheinbar || allem Anscheine nach einen mathematischen Satz aufstellen kann & fragen „ist der nun richtig oder falsch”? In diesem Falle fragt man eben || verlangt man eben nach einer Analyse des gegebenen Ausdrucks.

Es scheint nun aber auch Sätze der Mathematik zu geben von denen man man nicht weiß || sagt, man wisse nicht ob sie sich als richtig oder falsch beweisen lassen oder nicht. Solche Sätze handeln von „allen Zahlen” und das typische an ihnen ist daß in ihnen die Zahlen als eine Kollektion betrachtet werden & nicht als das Resultat vorgegebener Operationen. Es scheint dann als ob die Zahlen auch – gleichsam – zufällige Eigenschaften haben könnten die nämlich nicht in ihrem Wesen – in ihrem Bildungsgesetz – liegen & die man daher auch nicht voraussagen kann. [Ganz dasselbe Problem entsteht für den Raum]. Wenn ich z.B. die Dezimalen von π & die Reihe der natürlichen Zahlen vergleiche & frage ob sie nach dem ersten Glied noch jemals übereinstimmen werden: Was soll das heißen, wenn man diese Reihen in extenso auffaßt? Intentional betrachtet kann es heißen: „liegt es im Wesen der beiden Gesetze, daß etc.?”

Wie zeigt es sich, daß der Raum keine Kollektion von Punkten sondern die Verkörperung || Realisierung eines Gesetzes ist?

Es scheint mir daß der Begriff der Distanz in der Struktur des Gesichtsraumes unmittelbar gegeben ist. Wenn das nicht so ist & der Begriff der Distanz nur durch eine Korrelation des || eines distanzlosen Gesichtsraumes und einer anderen distanzhaltigen Struktur mit dem Gesichtsraum assoziiert ist, dann ist z.B. der Fall denkbar, daß durch eine Änderung dieser Assoziation z.B. die Strecke a

A         B              C |––––––|––––––––|     ︸      a         ︸           b

^(Ƒ) größer erscheint als die Strecke b obwohl wir den Punkt B noch immer zwischen A & B gewahren.

Obwohl uns Punkte im Gesichtsraum nicht gegeben sind so könnten wir doch – und vielleicht ist es das richtige – die Flächen gleichsam als Punktgewebe betrachten. D.h. der Punkt kommt im Zeichen als ein unselbständiger Bestandteil vor der aber die Struktur des Zeichens charakterisiert.

Es scheint mir als müsse man erst die ganze Raumstruktur ohne Sätze aufbauen; und dann kann man in ihr alle sinnvollen || korrekten Sätze bilden.

Man bekommt sicher die richtige Mannigfaltigkeit der Bezeichnungen wenn man sich der analytischen Geometrie bedient.

Wenn y = fx die Gleichung irgend einer geschlossenen Kurve ist und y hat zwei Werte für jeden Wert von x so schreibe ich eine beliebige Zahl im das Intervall zwischen zwei Werten von y – nämlich f₁x & f₂x – so: „f₁x,f₂x”. Dieses Zeichen ist eine Variable. Ich kann analog auch schreiben „4,5” d.i. die variable Zahl zwischen 4 & 5.
     „[a,b]” soll dann die Klasse aller Werte der Variablen a,b bezeichnen also das Intervall zwischen a & b. Dieses Intervall ist keine Klasse im Sinne Russells, denn es ist nicht durch eine Funktion gegeben & die Zugehörigkeit zum Intervall bestimmt sich nicht danach ob ein gewisser Satz wahr oder falsch ist. Ob etwas ein Glied des Intervalls ist läßt sich vielmehr aus dem Zeichen dieses Etwas erkennen. In gewissem Sinne ist das Intervall also tatsächlich eine „Klasse in extenso”, nämlich keine Intension die sich für eine Extension ausgibt. Ich könnte das Intervall auch eine interne Klasse nennen weil die Zugehörigkeit zum Intervall durch die internen Eigenschaften bestimmt wird.

(x; f₁x,f₂x) soll dann ein Zahlenpaar sein dessen eine Zahl x, die andere eine der Zahlen des Intervalls f₁x,f₂x ist.

Dieses variable Zahlenpaar entspricht dem was man einen Punkt der Fläche nennt.

Einem solchen Zahlenpaar ordne ich eine Funktion von x & f₁x, f₂x zu; das entspräche der Feststellung daß jeder Punkt des Flecks eine Farbe haben soll die von der Lage des Punktes im Fleck abhängt. Aber diese Zuordnung ist noch kein Satz denn ein Punkt kann gar keine Farbe haben. Vielmehr ist diese Zuordnung erst die Vorbereitung zu einem Satz.
     Der Satz entsteht vielmehr erst dadurch daß ich diese Zuordnung über den Fleck ausdehne.

     Statt des Flecks steht der Ausdruck: „[(x; f₁x,f₂x)]” das ist wieder eine interne Klasse wie das Intervall.

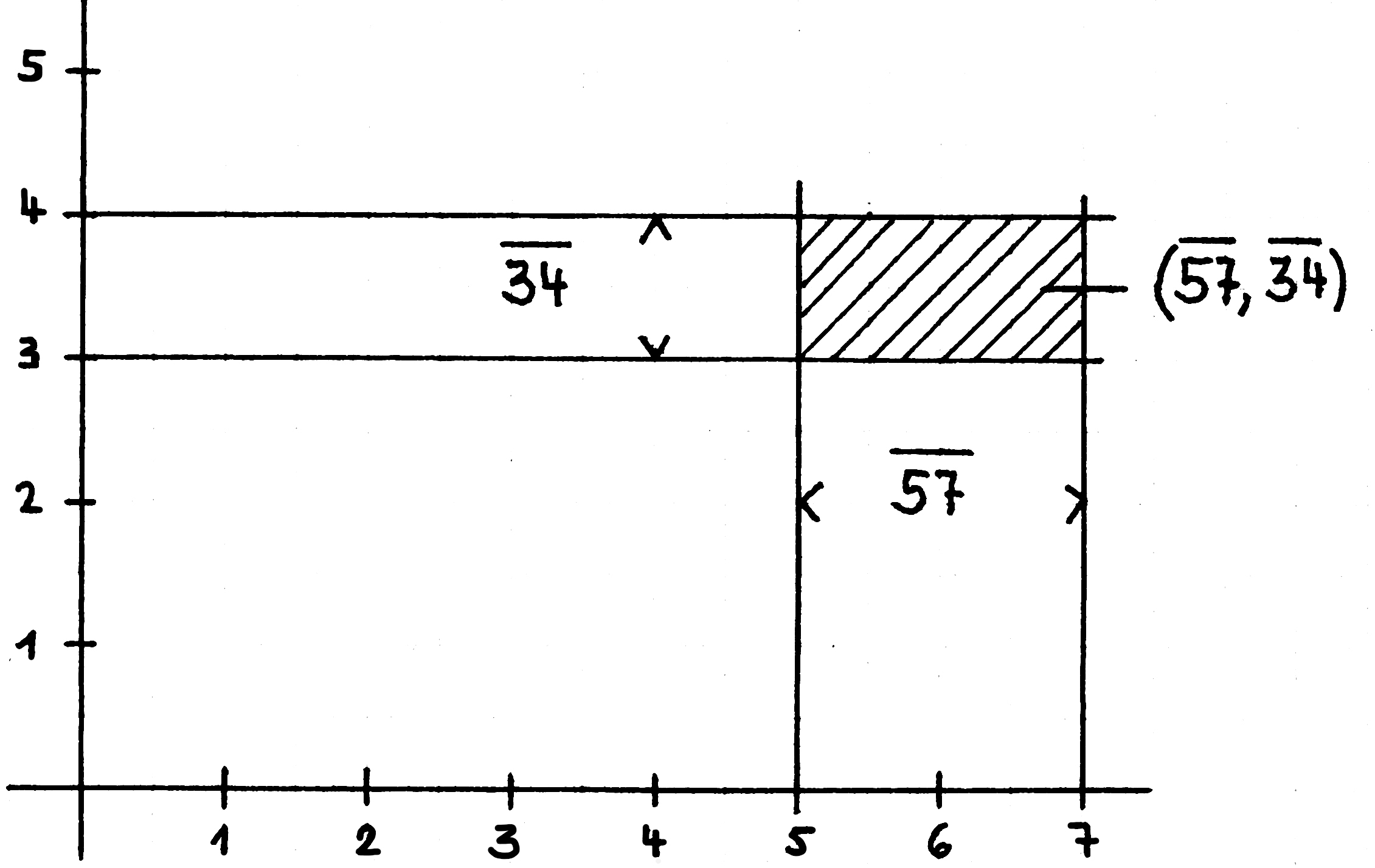
„[(x; f₁x,f₂x) ⬭ φ(x; f₁x,f₂x)]” ist erst der Satz der die Farbverteilung im Fleck [(x; f₁x,f₂x)] beschreibt. Wenn das Rechteck [(57,34)] || der rechteckige Fleck [(57,34)], einfärbig ist, etwa die Farbe hat die der Zahl N entspricht, so kann man diese Tatsache durch den Satz ausdrücken: [(57,34 ⬭ N)]

Wie aber würde es sich in dieser Notation zeigen können, daß ein Fleck nicht zwei Farben zugleich haben kann? Zeigt sich das nicht so ist etwas in der Notation falsch.

[Daß ein Punkt in der Ebene durch ein Zahlenpaar, im 3-dimensionalen Raum durch ein Zahlentrippel dargestellt wird zeigt schon daß der dargestellte Gegenstand gar nicht der Punkt sondern das Punktgewebe ist.]

Würde uns in der Schwierigkeit zu zeigen, daß nur nicht zwei Farben zugleich an einem Ort sein können die Erfahrung der Zeit etwas nützen?
     Angenommen unser Gesichtsbild bliebe immer dasselbe & andere Sinne als den Gesichtssinn hätten wir nicht, würde dann Zeit verrinnen?
     Man muß scheinbar annehmen: ja; denn der Wechsel schließt auch die Möglichkeit der Ruhe in sich.
     Obwohl es schwer ist sich zu denken daß Zeit vergeht wenn alles gleichbleibt.
     Aber schon zu sagen alles bleibt gleich setzt die Zeit voraus.

Zu sagen daß eine bestimmte Farbe jetzt an einem Ort ist, heißt diesen Ort vollständig beschreiben.

Wenn ich sage auf diesem Tisch liegen 4

Denken wir uns die Farbe als dritte Dimension so daß unsere Zeichenebene den Farbkörper, der in der dritten Dimension die Farbenskala durchläuft, in einer bestimmten Farbe schneidet so ist es klar daß die Ebene den Farbkörper nicht an verschiedenen Stellen schneiden kann.

Man könnte sagen: Was hat die & die Koordinaten? Eben die Farbe! Aber dann könnte man auch sagen diese Farbe hat diese Koordinaten & eine andere Farbe hat dieselben Koordinaten.

Die Bezeichnungsweise die ich oben vorgeschlagen habe könnte man auch verwenden wenn ein Zahlenpaar nicht einen Punkt sondern z.B. eine zur Zeichenebene senkrechte Gerade bezeichnen sollte & man könnte sich auf dieser Geraden verschiedene Farben der Länge nach aufgetragen denken. Und so könnten demselben Punkt mehrere Farben entsprechen.

Es verhält sich übrigens mit Farben nicht anders als mit Tönen oder elektrischen Ladungen.
     Es handelt sich immer um die vollständige Beschreibung eines gewissen Zustandes in einem Punkt oder zur selben Zeit.

Könnte es nicht folgendes Schema geben: Die Farbe in einem Punkt ist nicht durch die Zuordnung einer Zahl zu einem Punkt beschrieben sondern durch die Zuordnung mehrerer Zahlen. Eine Mischung dieser Zahlen macht erst die Farbe & um die vollständige Farbe zu beschreiben brauche ich den Satz daß diese Mischung nun die komplette Mischung ist, also nichts mehr dazu kommen kann. Das wäre so wie wenn ich den Geschmack eines Gerichtes beschriebe indem ich die Ingredienzien aufzähle; dann muß ich am Schluß den Zusatz machen daß das nun alle Ingredienzien sind.

So könnte man sagen ist auch die Farbe erst dann fertig beschrieben wenn alle ihre Ingredienzien angegeben sind, natürlich also mit dem Zusatz daß es alle sind.

Aber wie ist dieser Zusatz zu machen?!!

Wenn in Form eines Satzes, dann müßte auch die unvollständige Beschreibung der Farbe schon ein Satz sein.
     Und wenn nicht in Form eines eigenen Satzes sondern nur durch irgend eine Art der Andeutung im ersten Satz, wie kann ich dann bewirken daß ein zweiter Satz von der selben Form dem ersten widerspricht?
     Zwei Elementarsätze können einander ja nicht widersprechen!

Wie verhält es sich aber mit allen scheinbar ähnlichen Aussagen wie: Ein materieller Punkt kann nur eine Geschwindigkeit auf einmal haben, auf einem Punkt || in einem Punkt einer geladenen Oberfläche kann nur eine Spannung zugleich sein, in einem Punkt einer warmen Fläche nur eine Temperatur auf einmal, in einem Punkt eines Dampfkessels nur ein Druck etc. etc.

Niemand kann daran zweifeln daß das alles Selbstverständlichkeiten sind & die gegenteiligen Aussagen Unsinn. || Widersprüche.

Es scheint nun auf den ersten Blick zweierlei unter diesen Tautologien bezw. Kontradiktionen zu geben: Wenn man z.B. sagt ein Partikel könne nur eine Geschwindigkeit haben so kann man statt dessen auch sagen nur eine resultierende Geschwindigkeit || Gesamtgeschwindigkeit. D.h. die Beschreibung der Geschwindigkeit braucht einen abschließenden Zusatz wie oben. Allerdings hat es damit auch eine Schwierigkeit denn wie, nun, wenn die Geschwindigkeiten sich subtrahieren.
Sagt man andererseits daß zwei Punkte || Partikel nicht zugleich an derselben Stelle des Raumes sein können so ist das || scheint das in anderem Sinn selbstverständlich zu sein. Es scheint nämlich als ginge das aus der Definition eines Partikels hervor. Dann wäre also die gegenteilige Behauptung nicht ein Widerspruch sondern ein Unsinn.

Wie ist es nun im Falle der Farben: Nehmen wir an die Aussage die einem Fleck eine Farbe zuschreibt wäre die Aussage über eine gewisse Schwingungszahl dann könnte man die Sache auch so auffassen daß die Angaben verschiedener Schwingungszahlen einander nicht widersprechen, ebensowenig wie die Sätze: „es liegen 3 Äpfel auf dem Tisch”, „es liegen 5 Äpfel auf dem Tisch”; solange in keinem der Sätze das Wort nur vorkommt.
     Dem Satz der einem Fleck auch (und nicht nur) eine Schwingungszahl zuschriebe, entspräche also keine Farbangabe sondern etwas unbestimmteres, etwa analog einem Grad der Helligkeit.

Aber auch diese Erklärung ist ungenügend & zwar aus mehr als einem Grund.
     Wenn die Farben alle nur verschiedene Stadien derselben Struktur sind dann genügt es nicht daß aus „a ist rot” folgt „a ist nicht grün” sondern man muß auch ersehen daß eine Farbe einer anderen näher liegt als eine dritte, u.s.w..

Ginge es so daß man die resultierende Farbe als ein Zusammenwirken wirklich wahrgenommener Farben in verschiedenen Mischungsverhältnissen ansieht?
     Dann bestünde die Farbbeschreibung eines Flecks in einem logischen Produkt der Mischfarben & einem abschließenden Satz der sagt daß es alle Mischfarben || Sätze über die Elementarfarben & einem abschließenden Satz der sagt daß es alle Elementarfarben sind.

Haben aber nicht auch die Mischfarben || Elementarfarben eine Struktur? Und wie soll sich die zeigen?

Gibt es denn überhaupt Zeit im ersten System? Kann man von einem Ereignis oder vielmehr von einer Tatsache im System der Data sagen „es war”?

Wenn ich die Tatsachen des ersten Systems mit den Bildern auf der Leinwand & die Tatsachen im zweiten System mit den Bildern auf dem Filmstreifen vergleiche so gibt es auf dem Filmstreifen ein gegenwärtiges Bild, vergangene & zukünftige Bilder; auf der Leinwand aber ist nur die Gegenwart.

Das eine Charakteristische an diesem Gleichnis ist, daß ich darin die Zukunft als präformiert ansehe.

Es hat einen Sinn zu sagen die zukünftigen Ereignisse seien präformiert wenn es im Wesen der Zeit liegt, nicht abzureißen. Denn dann kann man sagen: „Etwas wird geschehen, ich weiß nur nicht, was”. Und in der Welt der Physik kann man das offenbar sagen.

Wie aber in der Welt der Data? Reißt diese Welt nicht wirklich ab?
Kann man von einem Datum sagen es sei früher als ein anderes?
Ich habe eben gegenwärtige Data || Sinnesbilder & gegenwärtige Erinnerungsbilder. Kann ich nicht sagen daß ich aus diesen nur im 2. System die Zeit konstruiere.
     Man kann aber auch sagen daß ich aus diesen gegenwärtigen Data ein zeitliches 2. System konstruieren kann sagt etwas von dem || über das 1. System aus & was es aussagt drücke ich in den Worten aus: Das

In der richtigen Darstellung der Farben muß sich nicht nur zeigen daß wenn a rot ist es nicht zugleich grün sein kann, sondern alle jene internen Eigenschaften müssen sich zeigen die wir kennen wenn wir die Farben kennen. Also alles was sich auf die Verwandtschaft der einzelnen Farben zueinander & ihr Verhältnis zu Schwarz & Weiß bezieht.

Hier macht die Farbenblindheit auf etwas aufmerksam || weist die Farbenblindheit auf etwas hin: Es gibt Leute die den Sinn für rot & grün oder für gelb & blau nicht haben. Daraus könnte man schließen daß man Gelb & Blau kennen kann ohne dadurch auf die Existenz || Möglichkeit von Rot & Grün schließen zu können, daß also diese Farbpaare logisch von einander unabhängig sind.

Es scheint einfache Farben zu geben. Einfach als psychologische Erscheinungen.
Was ich brauche ist eine psychologische Farbenlehre, keine physikalische & ebensowenig eine physiologische.

Und zwar muß es eine rein psychologische Farbenlehre sein in der nur von wirklich Wahrnehmbarem die Rede ist und keine hypothetischen Gegenstände , – Wellen, Zellen etc. etc. – vorkommen.

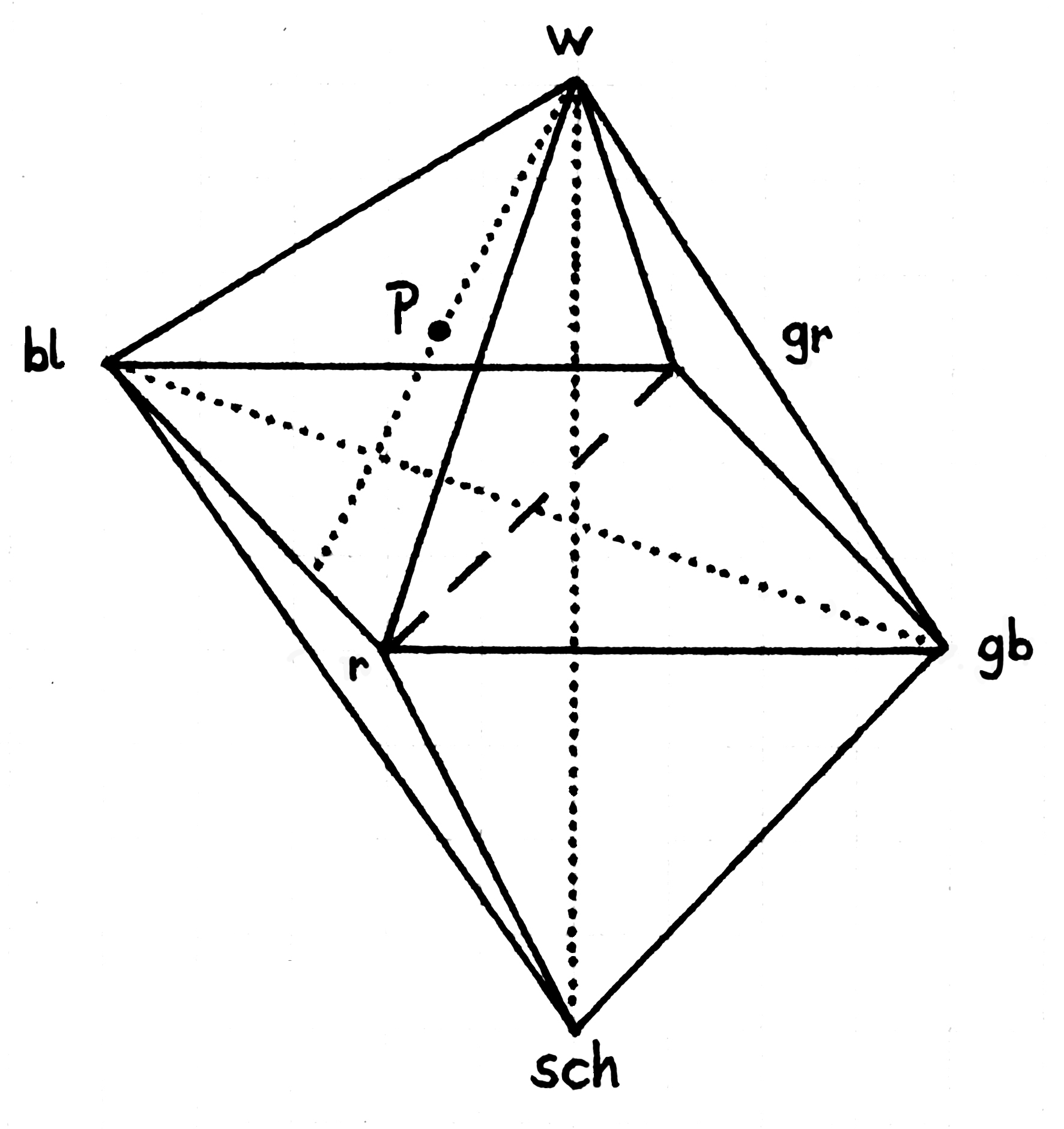
Man kann nun unmittelbar Farben als Mischungen von rot, grün, blau, gelb, schwarz, & weiß erkennen. Dabei ist Farbe immer Color nie pigmentum, nie Licht, nie Vorgänge auf oder in der Netzhaut etc.

Man kann auch sehen daß die eine Farbe röter ist als die andere oder weißlicher etc. Aber kann ich eine Metrik der Farben finden? Hat es einen Sinn zu sagen daß die eine Farbe etwa im || in Bezug auf ihren Gehalt an Rot in der Mitte zwischen zwei anderen Farben steht?

Es scheint jedenfalls einen Sinn zu haben zu sagen die eine Farbe steht einer anderen in dieser Beziehung näher als einer dritten. Und wenn dem so ist so hätte || hat es auch Sinn von der Mitte zwischen zwei Farben zu reden.
Das aber gäbe die Möglichkeit ein Farbintervall in gleiche Teile zu teilen solange allerdings nur bis die Grenze der Unterscheidbarkeit erreicht ist.
      Hier stoßen wir auf ein Problem das auch in der Ausdehnung des Gesichtsraumes auftritt nämlich des kleinsten sichtbaren Unterschieds. Die Existenz eines kleinsten sichtbaren Unterschieds widerspricht irgendwie der Kontinuität anderseits müssen sie sich miteinander vereinbaren lassen.

Wenn ich eine Reihe von Flecken hab die abwechselnd schwarz & weiß sind wie die Figur zeigt so werde ich bei weiterer Unterteilung bald zu einer Grenze kommen, wo ich die schwarzen & weißen Flecke nicht mehr unterscheiden kann, wo ich also etwa den Eindruck eines grauen Streifens habe.
     Heißt das aber nicht daß ich die Strecke in meinem Gesichtsfeld nicht beliebig unterteilen kann; und doch sehe ich keine Diskontinuität und auch das ist ja selbstverständlich weil ich eine Diskontinuität nur sehen könnte wenn ich noch nicht an der Grenze des Unterscheidbaren angelangt wäre.
     Das schaut sehr paradox aus.

Aber wie ist es denn mit der Kontinuität || Stätigkeit zwischen den einzelnen Reihen. Wir haben offenbar eine vorletzte Reihe von unterscheidbaren Flecken & dann die letzte einfarbig graue Reihe; ist es denn dieser letzten Reihe anzusehen daß sie wirklich durch Unterteilung der vorletzten entstanden ist? Offenbar nicht. Andererseits: Ist es aber der sogenannten vorletzten Reihe anzusehen daß sie nicht mehr sichtbar unterteilt werden kann? Es scheint mir, ebensowenig! Dann gäbe es also doch keine letzte sichtbar unterteilte Reihe!
     Wenn ich die Strecke nicht mehr sichtbar unterteilen kann, so kann ich aber auch nicht den Versuch dieser Unterteilung machen. Kann also auch nicht das Mißlingen eines solchen Versuches sehen.
     (Es ist hier wie mit der Grenzenlosigkeit des Gesichtsraums.)
     Dasselbe würde natürlich auch von den Farbenunterschieden gelten.

Die Kontinuität in unserem Gesichtsfeld besteht darin,¤ daß wir keine Diskontinuität sehen.

Wenn die Welt der Data zeitlos ist, wie kann man dann überhaupt über sie reden.

Wenn die Erinnerung kein Sehen in die Vergangenheit ist wie wissen wir dann überhaupt daß sie mit Beziehung auf die Vergangenheit zu deuten ist? Wir könnten uns dann einer Begebenheit erinnern & zweifeln ob wir in unserem Erinnerungsbild ein Bild der Vergangenheit oder der Zukunft haben.
Man kann natürlich sagen: ich sehe nicht die Vergangenheit sondern nur ein Bild der Vergangenheit. Aber woher weiß ich daß es || daß es ein Bild der Vergangenheit ist, wenn dies nicht im Wesen des Erinnerungsbildes liegt. Haben wir etwa durch die Erfahrung gelernt diese Bilder als Bilder der Vergangenheit zu deuten? Aber was hieße dann überhaupt || hier überhaupt „Vergangenheit”?!

Nun widerstreitet es aber allen Begriffen der physikalischen Zeit daß ich in die Vergangenheit wahrnehmen sollte & das scheint wieder nichts anderes zu bedeuten, als daß der Zeitbegriff im 1. System von dem in der Physik radikal verschieden sein muß.

Wenn man fragt: „Welches Erlebnis liegt dem Zeitbegriff, der Annahme einer Zeit, zugrunde || zu Grunde?” Wie muß man antworten? – Es ist die Erinnerung, wenn es eine punktartige Gegenwart gibt; oder es ist eine kontinuierliche Wahrnehmung deren einer Endpunkt die Gegenwart ist & die man in einem weiteren Sinne auch Erinnerung nennen könnte. || kann.

Jeder Punkt auf der Oberfläche des Oktaeders stellt eine Farbe dar z.B. P ein weißliches Blaurot welches näher dem Rot als dem Blau ist.

Eine räumliche Distanz kann durch eine Zahl dargestellt werden. (Dieser Satz handelt nicht von

Wie soll die Tatsache korrekt ausgedrückt werden daß φ( ) von ebensovielen Gegenständen befriedigt wird wie ψ( )?

^(Ƒ)
(x = a ∙ b = y) ⌵ (x = c ∙ d = y) Dies ist natürlich keine 1→1 Relation zwischen den beiden Klassen aber es ist der Ausdruck einer Regel nach der die Zeichen der Gegenstände einander zugeordnet werden können.

Wie kommt es, daß man Äpfel & Schuhe zählen kann, und auch Zahlen?!

Die Zahl ist ein Schema.

Wenn ich von der „Zahl der Bücher auf diesem Tisch” rede, so meine ich ein gewisses Schema von der Art ❘ ❘ ❘ ❘ … oder (0, ξ, ξ + 1), das sich auf den Umfang dieses Begriffes anwenden läßt. Unter dem Schema verstehe ich natürlich nicht die 4 Striche sondern dasjenige was ihnen mit allen Viererklassen gemeinsam ist, was ich aber nicht ohne eine solche darstellen kann.

a b c d
e f g h^(Ƒ)
Wenn ich zwei Viererklassen habe so könnte ich sagen: Daß diese Klasse gleichzahlig ist kann ich zeigen weil es möglich ist die Namen in Paare zusammen zu fassen die eine 1–1 Relation zwischen den Klassen etablieren.
     Ich kann also etwa schreiben a e, b f, e g, d h. Diese Möglichkeit der Zusammenfassung der Namen beweist natürlich etwas über die Klassen (nämlich ihre Gleichzahligkeit). Und genau dasselbe beweist auch die mögliche Zusammenfassung durch Identitäten (a = x ∙ y = e etc.).

(∃x,y,z) ∙ φx ∙ φy ∙ φz : ~(∃x,y,z,u) φx ∙ φy ∙ φz ∙ φu
Wie müßte ich es nun anfangen die allgemeine Form solcher Sätze zu schreiben?! Diese Frage hat offenbar einen guten Sinn. Denn wenn ich nur ein paar solche Sätze hinschreibe so versteht jeder was das Wesentliche dieser Sätze sein soll.

     Ich müßte offenbar eine Beschreibung dieses Wesentlichen des Zeichens geben.
Ich könnte etwa sagen in der linken || rechten Klammer kommen alle Buchstaben der linken Klammer vor und noch einer mehr. Aber ist so eine Beschreibung erlaubt? Merkwürdigerweise glaube ich, ja. Setzt nicht jeder Symbolismus solche Beschreibungen voraus?
     Ich könnte auch ein Zeichen konstruieren:



     Oder ich könnte die Regel geben:
Der Satz || Ausdruck (∃…) φ… ∙ ~(∃…) φ… ist eine Variable deren Werte der folgenden Beschreibung genügen: …. Hier kann man auch von einer 1-1 Relation Gebrauch machen als Kriterium dafür daß in der rechten Klammer alle Buchstaben der linken stehen.

Die Beschreibung der Zeichen der Werte der Variablen ist immer nur eine äußerliche Beschreibung. Sie ist die Beschreibung des Zeichens & nicht des Symbols.

Ich glaube das einzige was bei einer solchen Beschreibung des Zeichens unbedingt erforderlich ist, ist daß man von einem jeden Zeichen muß sagen können ob es einen Wert der Variablen darstellt oder nicht.

Ich sagte daß jeder Symbolismus eine solche Beschreibung || solche Beschreibungen voraussetzt. Wenn etwa Russell das Zeichen (∃x etc.) einführt so kann er nicht alle Zeichen
(∃x) etc., (∃x,y) etc., (∃x,y,z) etc. ad infinitum einführen sondern er gibt eine Regel die wir verstehen müssen, eine syntaktische Regel.

Ich führte keinen neuen Grundbegriff ein wenn ich die Variable (∃…) φ… ∙ ~(∃…) φ… konzipierte. Die Werte dieser Variablen sind ja wohlbekannt.

Können Unklarheiten & Widersprüche in der Beschreibung der Variablen vorkommen? Und wie sind sie zu vermeiden. Muß man hier so vorgehen wie Frege? Hier scheinen noch Schwierigkeiten zu liegen.

(∃x,y) φx ∙ φy ∙ ~(∃x,y,z) φx ∙ φy ∙ φz ≝ {ξ,ζ}φ(ξ)
Diese Definition bedarf zu ihrem Verständnis wieder einer Erklärung, denn die interne Beziehung zwischen den beiden Seiten ist nicht unmittelbar klar. (Wir wissen nicht worauf es in diesen Zeichen ankommt.)

(∃…) Könnte man diese Beschreibungen nicht mit Hilfe von Operationen geben?

Ein einfacherer Fall:
      φa ∙ φb ≝ P_a,b(φ)
      φa ∙ φb ∙ φc ≝ P_a,b,c(φ)
      φa ∙ φb ∙ φc ∙ φd ≝ P_a,b,c,d(φ)
Nun will ich allgemein das variable Produkt P_…(φ) definieren! Wie soll ich das machen?
Man könnte eine Operation hinschreiben:
[φa ∙ φb = P_a,b(φ); – = P_(φ), – ∙ φη = P_{_,η}(φ)]

Diese Operation ist offenbar nur eine äußerliche || äußere Beschreibung der Zeichen.
     Das Wesen der Sache muß ich dann – gleichsam – von selbst verstehen. Denn die Operation gibt es mir nicht. Sie behandelt nämlich die Zeichen als ob sie sinnlos wären. Ich könnte ebensogut hinschreiben
[∃,–,–0] & dies würde die Reihe ∃,∃0,∃00 etc. darstellen die gar nichts heißt.

Ist das aber in Ordnung?

Die Glieder der Operationsreihe haben ja Bedeutung & ihre interne Verwandtschaft ist keine äußerliche Angelegenheit der Zeichen sondern eine Verwandtschaft der Bedeutungen. Dieser Verwandtschaft muß also eine Verwandtschaft der Symbole & nicht nur der Zeichen entsprechen. Muß nicht offenbar der Übergang von einem Zeichen zum nächsten ein sinnvoller Übergang sein?

Wie ist es mit der Operation die die Reihe
(∃x) φx, (∃x,y) φx ∙ φy, etc. hervorbringt? Sie wäre:

Aber hier ist eine Schwierigkeit darin daß ich nicht ausgedrückt habe daß das hinzukommende ξ von allen früheren Zeichen verschieden sein muß. Ist das nicht eine fundamentale Schwierigkeit?

Definitionen:
(∃x,y) φx ∙ φy ≝ (∃α,α)φα
(∃x,y,z) φx ∙ φy ∙ φz ≝ (∃α,α,α)φα etc. || .
allgemein:
[(∃x,y) φx ∙ φy, = (∃α,α)φα, (∃–) ∙ – = (∃–)φα, (∃–ξ) ∙ – ∙ φξ = ¤ (∃–,α)φα].
     Dann wäre die allgemeine Form von
(∃α)φα, (∃α,α)φα, etc.:
[(∃α)φα, (∃–) ∙ φα, (∃–,α) ∙ φα]

(∃α)φα ∙ ~(∃α,α) ∙ φα = (Nα)φα
(∃α,α)φα ∙ ~(∃ααα)φα = (Nα,α)φα
[(∃α)φα ∙ ~(∃α,α) ∙ φα = (Nα)φα, (∃–)φα ∙ ~(∃–)φα = (N–)φα, (∃–,α)φα ∙ ¤~(∃–,α)φα = N(–,α)φα].
So wäre das Zeichen N(…)φα einzuführen.

Die Allgemeine Form der Zahlenaussage wäre dann:

[(Nα)φα, (N–)φα, (N–,α)φα]

Erinnern wir uns: In der Arithmetik kommt die Zahl allein ohne den Begriff vor zu dem sie gehört. Dann ist sie aber doch ein unvollständiges Zeichen. Aber so kommt sie ja auch nie in einem Satz vor, im Satz ist sie immer mit einem Begriff verbunden. Kein Satz handelt von der Zahl 4. In der Arithmetik aber wo die Zahlen für sich vorkommen stehen sie aber auch nicht in Sätzen.

Das Zahlzeichen ist ein Schema & ist in der Arithmetik aus seinem Zusammenhang gerissen.

[(Nα)φα, (N–)φα, (N–,α)φα] ≝ (α,–,–,α)φα

Dann könnte man die Funktion „(α,–,–,α)( )” die allgemeine Form der Zahl nennen. Die leere Klammer deutet an daß es sich um das Gemeinsame aller Zahlenaussagen handelt.

Die Zahlen sind Bilder der Begriffsumfänge.

Man kann fragen hat denn die Zahl wesentlich etwas mit einem Begriff zu tun? Ich glaube das kommt darauf hinaus zu fragen ob es einen Sinn hat von einer Anzahl von Gegenständen zu reden die nicht unter einen Begriff gebracht sind. Heißt es z.B. etwas zu sagen:
„a und b und c sind 3 Gegenstände”? Ich glaube, offenbar, nein! Es ist allerdings ein Gefühl vorhanden das uns sagt: Wozu von Begriffen reden; die Zahl hängt ja nur vom Umfang des Begriffes ab und wenn der einmal bestimmt ist, so kann der Begriff so zu sagen abtreten. Der Begriff dient nur als Methode || ist nur eine Methode um einen bestimmten Umfang zu bestimmen, der Umfang aber ist selbständig und in seinem Wesen unabhängig vom Begriff; denn es kommt ja auch nicht darauf an durch welchen Begriff wir den Umfang bestimmt haben. Das ist das Argument für die extensionale Auffassung. Dagegen kann man zuerst sagen: Wenn der Begriff wirklich nur ein Hilfsmittel ist um zum Umfang zu gelangen, dann hat der Begriff in der Arithmetik nichts zu suchen; dann muß man eben die Klasse gänzlich von dem zufällig mit ihr verknüpften Begriff scheiden. Im umgekehrten Fall aber ist der vom Begriff unabhängige Umfang nur eine Chimaire & dann ist es besser von ihm überhaupt nicht zu reden sondern nur vom Begriff.

φa ∙ φb ∙ φc ∙ φd ≝ (a,b,c,d) ∙ {φ( )}
     Könnte ich nun nicht das unvollständige Zeichen (a,b,c,d) ∙ { } den Umfang des Begriffes ξ nennen für den (a,b,c,d) ∙ {ξ( )} wahr wird?

     Die Zahl (αααα) wäre dann das allgemeine Schema des Umfangs (a,b,c,d) ∙ { }.

Man könnte nun den Begriffsumfang wie einen Gegenstand betrachten dessen Name ja auch nur im Zusammenhang || Satzzusammenhang Sinn hat. „a und b und c und d” ist allerdings sinnlos || hat allerdings keinen Sinn, das ist kein Satz. Aber „a” ist ja auch kein Satz.

Hat es nun aber einen Sinn eine beliebige Form eines Begriffsumfangs hinzuschreiben etwa (a,g,i,u) ∙ { }, wo die Buchstaben in der Klammer Namen von bestimmten Gegenständen sein sollen, wenn ich gar nicht weiß ob diese Gegenstände „unter einen Hut zu bringen” sind?
     Kann man darauf nicht antworten: Daß ein Name Bedeutung hat setzt voraus daß er in einem Satz Sinn hat; d.h. die Namen könnte man eigentlich schreiben ξ(a), ξ(i), ξ(u) etc. wo ξ eine variable Funktion ist. Dann aber muß auch das Zeichen für den Begriffsumfang immer zulässig sein.

Folgt nun daraus nicht daß, wenn ich aus den Schemata für die Begriffsumfänge, den Zahlen, durch irgendwelche || nach irgendwelchen Regeln neue solche Schemata bilde, daß diesem Übergang von der einen Zahl zur anderen auch ein möglicher Übergang in den Begriffsumfängen entsprechen muß da ich ja mit || in meinen Zeichen gerade mit dem Wesentlichen operiere.

Wie muß nun z.B. die Regel für die Bildung der Summe zweier Zahlen lauten?

Wenn ich zwei Umfänge u₁, u₂ habe so ist es offenbar daß das Zeichen (u₁, u₂){ } einen Sinn hat, merkwürdigerweise ohne daß ich irgend eine Konvention über die Addition von Begriffsumfängen vorher festgesetzt habe.

Ich habe einen instinktiven Wunsch nur mit den Begriffsumfängen zu operieren & von den Funktionen keine Notiz in der Arithmetik zu nehmen.
     Ich möchte es den Operationen mit den Zahlen dann selbst überlassen etwas zu bedeuten.

Jede Zahl kann man auffassen als aus mehreren anderen bestehend. [dieser Satz schaut dümmer aus als er ist.]

(Die russische Rechenmaschine)

Es scheint mir nämlich daß die Zerlegung einer Zahl in ihre Summanden eine unmittelbar einleuchtende Operation ist & nicht einer Einführung auf dem Umweg über Operationen mit Wahrheitsfunktionen bedarf.
     Es scheint mir also als ob man direkt sagen könnte „Siehst Du, ❘ ❘ ❘ ❘ besteht aus ❘ ❘ und ❘ ❘”.

Kann ich denn aus beliebigen Dingen einen Umfang bilden, ist es denn sicher daß es eine Funktion gibt deren Umfang er ist? Sätze die mit solchen beliebigen Umfängen gebildet werden, werden im allgemeinen nicht wahr sein aber es sind immer Sätze. Denn wenn es auch nicht wahr ist

Die Definition des Begriffsumfangs die ich oben gegeben habe stimmt übrigens gar nicht, sie müßte etwa lauten:

φa ∙ φb ∙ φc ∙ ~(∃x,y,z,u) ∙ φx ∙ φy ∙ φz ∙ φu = (a,b,c){φ( )}

Es hat gewiß Sinn von jedem Begriff zu sagen daß er z.B. 4 Gegenstände umfaßt auch wenn er nicht 4 Gegenstände umfaßt.
Insofern muß jedes Zeichen für Begriffsumfänge || Umfangszeichen erlaubt sein.

Wenn nun z.B. zwei Umfänge ganz außerhalb einander liegen so zeigt sich das in ihren Zeichen & wir brauchen ja dürfen zu dieser Konstatierung nicht auf die Begriffe zurückgehen da wir eben nicht wissen ob es solche Begriffe überhaupt gibt.

Zwischen den Begriffsumfängen werden vielmehr interne Relationen bestehen die man erweiterte Identitäten nennen könnte. Man könnte etwa schreiben
(a,b,c)

a =

(a,e,f)^(Ƒ) d.h., die beiden Umfänge sind in bezug auf a identisch.

Brauche ich jetzt nicht Zeichen für die allgemeine Form der Umfänge: die ein Glied gemeinsam haben, die kein Glied gemeinsam haben, von denen der eine den anderen ganz enthält, etc.?

Die Summe zweier Umfänge ist doch ein Umfang der die beiden anderen enthält und sonst kein Glied. Wie soll das ausgedrückt werden?

Dann brauche ich eine Art Definition die besagt daß ein gewisses Zeichen als Wert einer gewissen Variablen gebraucht wird.
     Etwa nε(α,–,– ∙ α) was etwa besagt daß ich „n” als Zahlzeichen verwenden werde.

Könnte man etwa festsetzen daß Umfänge die ganz außerhalb einander liegen einfach durch verschiedene Buchstaben benannt werden sollen; dagegen solche die gemeinsame Glieder haben durch gemeinsame Indexe als solche bezeichnet werden sollen.

u₁ = (a…) würde heißen u₁ enthält a
u₁ = (u₂…) u₁ enthält u₂
u₁ = (u₂,u₃,…) u₁ enthält u₂ & u₃
u₁ = (u₂,u₃) u₁ ist die Summe aus u₂ & u₃ etc.

(αααα) = ((ααα))¤(α))
αααααα = ((αα)(αα)(αα)) = ααα × αα

(n) = α × n
(n,n) = αα × n
– – – – – –
[(n) = α × n, (–) = – × n, (–,n) = –α × n] Das gäbe die Definition der Multiplikation.

[(n) = 1 × n, (–) = – × n,(–,n) = –, 1 × n] = m ∙ n

Es ist merkwürdig daß man im Fall der Tautologien & Kontradiktionen wirklich von Sinn & Bedeutung im Sinne Freges reden könnte.

Wenn man die Bedeutung der Tautologie ihre Eigenschaft eine Tautologie zu sein nennt dann kann man den Sinn der Tautologie die Art & Weise nennen wie hier die Tautologie zustande kommt. Das gleiche für die Kontradiktion.

Wenn man wie Ramsey vorschlägt das Zeichen „ = ” so erklärt daß ist, dann kann man sagen daß hier die Tautologie & die Kontradiktion keinen „Sinn” haben.

Wenn also die Tautologie dadurch etwas zeigt daß gerade dieser Sinn diese Bedeutung ergibt, so zeigt die Tautologie bei Ramsey nichts, denn sie ist Tautologie ex definitione.

Ramsey schlägt vor den Satz daß unendlich viele Gegenstände eine Funktion befriedigen dadurch auszudrücken daß er || daß er alle Sätze verneint von der Form:
~(∃x) φx
(∃x) φx ∙ ~(∃xy) φx ∙ φy
(∃xy) φx ∙ φy ∙ ~(∃xyz) φx ∙ φy ∙ φz
etc.^(Ƒ)
Aber nehmen wir nun an daß es nur 3 Gegenstände gibt d.h. daß nur 3 Namen Bedeutung haben. Dann können wir den dritten || vierten Satz der Reihe gar nicht mehr hinschreiben denn es hat dann keinen Sinn zu schreiben
~(∃x y z u) φx φy φz φu ⁵

Wie muß aber nun eine zweckmäßige Notation der mathematischen Allgemeinheit aussehen?

Und da erhebt sich noch eine wichtige Frage: Kann die mathematische Allgemeinheit überhaupt anders auftreten als in unmittelbarer Verbindung mit dem Gleichheitszeichen? Kann es also || D.h. kann es Sätze geben von der Art (x) ∙ (∃y) f₁(x,y) ⌵ f₂(x,y) wo || wo die Allgemeinheit || der Bereich der Allgemeinheit notwendig über die Disjunktion ausgedehnt werden müßte? und der Satz nicht in eine Wahrheitsfunktion allgemeiner Gleichungen aufzulösen wäre?

Das scheint hier unmöglich zu sein.

x + y = 2            (x + y)² = 2(x² + y²)
x ‒ y = 3                x = y

     Haben wir hier nicht schon solche Fälle?!
(∃x,y)x + y = 2 & x ‒ y = 3

(n):n = 2 . ⊃ . (∃x,y,z) x² + y² = z²
Freilich sagt (∃x,y,z) nur, daß es beweisbar ist, daß x² + y² = z² Lösungen hat & bezieht sich nicht auf die Angabe bestimmter Zahlen, noch kann es durch diese Angabe bewiesen werden!

(Ich ahne daß es möglich sein wird ohne Wahrheitsfunktionen auszukommen)

Der Fermatsche Satz ist (n): n ≠ 2 ⌵ n ≠ 1 ¤ ⊃ ~(∃x,y,z) xⁿ + yⁿ = zⁿ oder (n):(∃x,y,z) xⁿ + yⁿ = zⁿ ∙ x ≠ 0 ∙ y ≠ 0 ∙ z ≠ 0 . ≡ . n = 1 ⌵ n = 2

Was aber wird nun aus meiner Auffassung der Variablen als allg. Konstante & Unbekannte?

Es ist klar daß ich die Konstruktion der mathematischen Satzzeichen dadurch erklären

So habe ich oben auch die Zeichen^(Ƒ) „(∃x)” und „(x)” behandelt. Nur treten jetzt die Wahrheitsfunktionen hinzu.

Kommen wir hier zu dieser Transformation von „(x)(∃y)y = 2x” in „(x)(∃2x)” die ich einmal angedeutet habe? (Die Möglichkeit der Verwandlung eines Relativsatzes in ein Attribut in der Allgemeinheit der Mathematik.)

(x): x² = 4 . ≡ . x = + 2 ⌵ x = ‒ 2 heißt: „rechne ‚(?)² = 4’ aus (d.h. nicht probieren) und du erhältst +2 und ‒ 2” (und zeigt hier nicht das „und”^(Ƒ) daß die Wahrheitsfunktion in diesen Sätzen nicht wesentlich vorkommt?)

ξ definiert durch die Gleichung

Unbekannte x²

= 4^(Ƒ), hat die Werte 2 und ‒ 2

(Ramsey versteht den Wert den ich auf eine bestimmte Notation lege ebensowenig, wie den Wert den ich auf ein bestimmtes Wort lege, weil er

Es muß eine Beziehung zwischen beiden Auffassungen der Variablen geben.

(a + b)² = a² + xab + b² ergibt x = 2 (x + b)² = x² + 2xb + b² ergibt x = x

}

und beide bedeuten denselben Sachverhalt der auch in (a + b) = a² + 2ab + b² behauptet wird [ist das aber wahr?]

Könnte ich statt „(∃x) x² + 3x + 2” auch schreiben (

‒ 2 ‒ 1

)² + (

‒ 2 ‒ 1

) ∙ 3 + 2 = 0 (wobei (

‒ 2 ‒ 1

) als das Resultat der Ausrechnung aufgefaßt wird)?

Ich sehe noch kein System in allen diesen Fragen.

Ich könnte den Fermatschen Satz so schreiben: „Die Gleichung xⁿ + yⁿ = zⁿ ergibt die Lösung:

{	x = 0, y = 0, z = 0, n = n x = r, y = s, z = r + s, n = 1 x = r² ‒ s², y = 2rs, z = r² + s², n = 2

Kann man aber nicht sagen: Wie aber, wenn eben diese Frage unentscheidbar wäre? Ja, wie, wenn in einem Falle die Frage, ob fa = φa der Fall ist, unentscheidbar wäre? Etwa angenommen es hätte uns jemand den Satz e^2πi = 1 hinterlassen ohne Beweis & wir zerbrächen uns die Köpfe ob es so ist oder nicht; und jemand sagte: „aber vielleicht ist das unentscheidbar”!

Es ist klar, ich kann nur dort den allgemeinen Satz (mit den allg. Konstanten) hinschreiben wo er dem Satz 25² = 625 analog ist, und das ist, wo ich die Rechnungsregeln für a & b ebenso kenne wie die Rechnungsregeln für 6, 2, & 5. Das illustriert ganz, was es heißt, daß a & b hier konstante sind: Konstante Formen nämlich.

Aber was heißt es denn, die Rechnungsregeln zu kennen?!

Ist es so: Ich kann das Wort „ergibt” nicht anwenden, solange ich keine Methode der Lösung kenne, weil ergibt eine Struktur bedeutet die ich nicht ohne sie zu kennen bezeichnen kann. Weil die Struktur dargestellt werden muß.

Ich habe die intensive Auffassung noch immer nicht ganz durchgeführt!

Jeder Satz ist die Anweisung auf einen Beweis || eine Verifikation.

Wonach darf ich denn in der Mathematik fragen?

Ich darf doch, bei aller Bescheidenheit, in irgend einem Sinne nach dem Verhältnis der Grundregeln zu einem – scheinbar – mathematischen Satz fragen.
     Hat diese Frage keinen Sinn so hat keine Frage in der Mathematik Sinn.

Wenn ich das Wort „ergibt” wesentlich intensional

Ich habe hier nichts anderes als den alten Fall, daß ich nicht sagen kann zwei Komplexe stünden in einer Relation ohne die Relation logisch abzubilden.

„Die Gleichung ergibt a” heißt: Wenn ich die Gleichung nach gewissen Regeln transformiere erhalte ich a, so wie die Gleichung 25 × 25 = 620 besagt, daß ich 620 erhalte wenn ich auf 25 × 25 die Regeln || Multiplikationsregeln anwende. Aber diese Regeln müssen mir schon gegeben sein, ehe das Wort „ergibt” Bedeutung hat & ehe die Frage einen Sinn hat, ob die Gleichung a ergibt.

Der Fermatsche Satz hat also keinen Sinn solange ich nach der Auflösung der Gleichung durch Kardinalzahlen nicht suchen kann.

Und „suchen” muß immer heißen: systematisch suchen. Es ist kein Suchen, wenn ich im unendlichen Raum nach einem Goldring umherirre.

An aller || unserer Schwierigkeit ist größtenteils die falsche Auffassung der Variablen schuld, nämlich die Auffassung als verträte sie Zahlen (die extensive Auffassung), während sie nichts vertritt sondern ist was sie ist. Verträte sie Zahlen dann brauchte allerdings nur 5³ + 7³ = 9³ Sinn haben & der Sinn der allgemeinen Sätze über die Form xⁿ + yⁿ = zⁿ folgte daraus. Aber da die Variable autonom ist, so hat der Satz mit ihr erst dann Sinn, wenn er nach seinen eigenen Prinzipien kontrollierbar ist wie 5³ + 7³ = 9³ nach den seinen.

Das⁷ Wort „Variable” ist zu ersetzen durch das Wort „Zahlform”. Und diese Form ist ebenso konstant, wie die Zahl 4.

Auch die Frage „Ist 5 + 7 = 13?” könnten wir nicht aufwerfen, wenn nicht 5, 7 & 13

Es wäre dann so wie mit Brouwers Pendelzahl von der man nicht entscheiden kann ob sie größer oder kleiner als 0 ist. Das heißt aber natürlich, daß man diese Frage nicht aufwerfen kann. Denn „wo sich nicht suchen läßt, da läßt sich auch nicht fragen”.

Es genügt also nicht zu sagen p ist beweisbar, sondern es muß heißen: beweisbar nach einem bestimmten System.

Und zwar behauptet der Satz nicht p sei beweisbar nach dem System S sondern nach seinem System, dem System von p. Daß p dem System S angehört, das läßt sich nicht behaupten, das muß sich zeigen.

Man kann nicht sagen p gehört zum System S;

Ich brauche kaum zu sagen daß dort, wo der Satz des ausgeschlossenen Dritten nicht gilt, auch kein anderer Satz der Logik gilt, weil wir es dort nicht mit Sätzen der Mathematik zu tun haben. (vergl. dagegen Weyl & Brouwer)

Würde denn aus dem Allen nicht das Paradoxe folgen, || : daß es in der Mathematik keine schweren Probleme gibt, weil was schwer ist, kein Problem ist?

Ganz so ist es aber nicht: Die schwierigen Probleme der Mathematik sind die, für deren Lösung wir noch kein geschriebenes System besitzen. Der suchende Mathematiker hat dann ein System in irgendwelchen psychischen Symbolen, Vorstellungen, „im Kopf” & trachtet es aufs Papier zu bringen. Hat er das getan so ist das Übrige leichter. Hat er

Nur Was man anfassen kann ist ein Problem.

Nur wo ein Problem sein kann, kann etwas behauptet werden!

Kenne ich die elementaren Regeln der || Regeln der elementaren Trigonometrie so kann ich den Satz sin 2α = 2 sin α cos α kontrollieren aber z.B. nicht den Satz sin x = 1 ‒

x³ 3!

+ … Das heißt aber, daß der sin der elementaren Trigonometrie & der der höheren verschiedene Begriffe sind. Wenn wir sie gleich benennen so hat das allerdings den guten Grund daß ¤ der zweite Begriff die Mannigfaltigkeit des ersten in sich schließt; aber für das System der elementaren Trigonometrie hat der zweite Satz keinen Sinn & die Frage ob sin x = 1 ‒

x³ 3

+ …

Die beiden Sätze stehen gleichsam auf zwei verschiedenen Ebenen. In der ersten kann ich mich herum bewegen so viel ich will, ich werde nie zu dem Satz der höheren Trigonometrie kommen.

Ist es nun eine richtige Frage, ob die Dreiteilung des Winkels möglich ist? Und welcher Art ist also der Satz & sein Beweis daß sie mit Zirkel & Lineal nicht möglich ist?

Man könnte sagen: Da sie nicht möglich ist konnte man auch nie nach ihr suchen.

Solange ich nicht das große System sehe, das beide umfaßt, kann ich das höhere Problem nicht zu lösen trachten.

Ich kann erst dann fragen ob der Winkel mit Lineal & Zirkel dreigeteilt werden kann, wenn ich das System „Lineal & Zirkel” in ein größeres eingebettet sehe, worin das Problem lösbar ist; oder vielmehr worin das Problem ein Problem ist, worin diese Frage einen Sinn hat.
     Das zeigt sich auch darin, daß man zum

Ein System ist sozusagen eine Welt.

Oder auch: Jedes höhere System ist eine Welt von mehr Dimensionen als das niedere.

Ein System kann man also nicht suchen. Wohl aber den Ausdruck für ein System das mir in ungeschriebenen Symbolen gegeben ist.

Der Schüler dem das Rüstzeug der elementaren Trigonometrie zur Verfügung stünde & von dem die Überprüfung der Gleichung sin x = 1 +

x³ 3!

… verlangt würde, fände das, was er zur Bewältigung dieser Aufgabe braucht eben nicht in geschriebenen Symbolen || geschrieben vor. Wenn der Lehrer dennoch die Lösung von ihm erwartet, so setzt er voraus, daß die Mannigfaltigkeit der Syntax die diese Lösung voraussetzt, in anderen Symbolen dem Schüler zur Verfügung steht || irgendwie in anderer Form im Kopf des Schülers vorhanden ist. Und zwar so, daß der Schüler den Symbolismus

Das System von Regeln welche einen Kalkül bestimmen, bestimmt damit auch die „Bedeutung” seiner Zeichen. Richtiger ausgedrückt: Die Form & die syntaktischen Regeln sind äquivalent. Ändere ich also die Regeln – ergänze ich sie etwa scheinbar – so ändere ich die Form, die Bedeutung.

Die Grenzen meiner Welt kann ich nicht ziehen, wohl aber Grenzen innerhalb meiner Welt. Ich kann nicht fragen, ob der Satz p zum System S gehört, wohl aber ob er zum Teil s von S gehört. Ich kann also dem Problem der 3-Teilung des Winkels im großen System seinen Platz bestimmen, aber nicht im Euklidischen System danach fragen ob es lösbar ist. In welcher Sprache sollte ich denn danach fragen? In der Euklidischen? Und ebensowenig kann ich in der Euklidischen Sprache^﹖ nach der Möglichkeit der 2-Teilung des Winkels im Euklidischen System fragen.

Hier liegt aber nichts vor was wir als eine Hierarchie von Typen bezeichnen dürften.

Man kann in der Mathematik nicht allgemein von Systemen sondern nur in Systemen reden. Sie sind gerade das, wovon man nicht reden kann. Also auch das, was man nicht suchen kann.

Der Schüler der den Apparat zur Beantwortung der zweiten Frage nicht hat, kann sie nicht nur, nicht beantworten, sondern, er kann sie auch nicht verstehen.

Das wäre ähnlich wie die Aufgabe die der Fürst im Märchen dem Schmied stellt ihm einen Klamank zu bringen.

Jeder rechtmäßige Satz der Mathematik muß, wie der Satz 12 × 13 = 137, an sein Problem die Leiter anlegen, || – die ich dann hinaufsteigen kann, wenn ich will.
     Das gilt von Sätzen aller Art der Allgemeinheit.

Man könnte auch sagen: „(a + b)² = a² + 2ab + b²” sagt daß die Lösung der Gleichung nach a + b a = a & b = b ergibt. x² + 2x + 3 = 0 sagt, daß die Lösung bestimmte Zahlen ergibt, wenn es nicht nur eine Frage ist.

Daß es einen Prozeß der Lösung gibt kann man nicht behaupten, || . Denn gäbe es den nicht, so wäre die Gleichung als allgemeiner Satz unsinnig.
     Man kann alles behaupten, was sich durch die Tat kontrollieren läßt.

Es handelt sich um die Möglichkeit der Kontrolle.

Eine Gleichung wie x² = 2x, als Aufgabe gestellt, ist keine Behauptung. Lies sie als Behauptung, dann sieht man es. Wenn Einer dem ich sie als Aufgabe hinschriebe, sie im Tonfall der Behauptung läse, würde ich sagen: „nein, so meine ich es nicht”.

x² +

2x b

+

3 c

= 0, x = ‒

b 2

± √

b² 4

‒ c

Die beiden^(Ƒ) Gleichungen so geschrieben geben offenbar die volle Antwort auf die Frage die in der ersten ausgedrückt ist.

Wenn in der Logik eine Frage 1.) allgemein & 2.) im Besonderen beantwortet werden kann, dann muß sich die besondere Beantwortung immer als ein Sonderfall der allgemeinen ausweisen; oder anders, || : der allgemeine Fall muß immer schon den besonderen als Möglichkeit in sich tragen.
     Ein Fall hiervon ist die Berechnung des

Wenn ich (∃x) x² = 2x schreibe & es || (∃x) nicht extensiv verstehe, so kann es nur behaupten: „Wenn ich die Regeln der Lösung anwende, so komme ich zu einer bestimmten Zahl im Gegensatz zu dem Falle, wo ich zu einer Identität oder einer verbotenen Gleichung komme”.

Wie ist die rein technische Verifikation von (x): x² = 2x ⊃ x = 0 ⌵ x = 2?
     Ich rechne x aus einer Gleichung aus, setze den Wert überall ein & muß dann einen wahren Satz erhalten.

Ergibt also die bloße Transformation von „x² = 2x” den Satz „x = 0 ⌵ x = 2”?

Gibt „x² = + 4”, „x = + 2 ⌵ x = ‒ 2”? D.h. sind die Wahrheitsfunktionen nötig? Oder auch: Liefert die Transformation nach den Regeln die beiden Gleichungen in der Verknüpfung „x = + 2 ⌵ x = ‒ 2”?

Was aber will das „(x)” in „(x): x² = 2x ⊃ x = 0 ⌵ x = 2”?
(Es wäre lächerlich es extensiv aufzufassen.) Ist es eine allg. Konstante? Jedenfalls keine Unbekannte.
Daß der Satz der bei der Ausrechnung herauskommt wahr ist, läßt sich wieder rein technisch durch Ersetzungsregeln – a = a … W, a ≠ a … F oder dergl. – zeigen. Dann ist also auch hier das x eine allg. Konstante.

Aber was ist denn die Verifikation von (∃x)x² = 2x? Ich meine die spezifische Verifikation dieser Gleichung || dieses Satzes, im Gegensatz zur Verifikation von „(x): x² = 2x ⊃ x = 2 ⌵ x = 0”.
Denn muß nicht der andere Satz – d.h. der andere Sinn – auch anders verifiziert werden? Etwa, der allgemeinere, allgemeiner.

„p ⌵ ~p” darf ich nur dann sagen wenn ich „p” verstehe; so darf ich sagen „5 × 5 = 11 ⌵ 5 × 5 ≠ 11” & die Allgemeinheit des Satzes macht gar keinen Unterschied. Ich könnte Zahlengleichungen & Buchstabengleichungen dahin zusammenfassen: Die Transformation der linken Seite nach den Regeln liefert die rechte Seite oder nicht.

Dazu müssen aber die beiden Seiten der Gleichung
     (N.B.: der allgemeinen) – sozusagen – kommensurabel sein.

Weil die Zahlengleichung f₁5 = f₂3 kommensurable Seiten hat, folgt nicht, daß f₁a = f₂b kommensurable Seiten haben muß. Denn für a & b gelten andere Rechnungsregeln als für 3 & 5.

Die Klassifikationen die Philosophen & Psychologen machen sind so wie wenn man Wolken nach ihrer Gestalt klassifizieren wollte.

Die Aufgabe der Philosophie ist, das erlösende

Meine Art des Philosophierens ist mir selbst immer noch – || , & immer wieder, neu, & daher muß ich mich so oft wiederholen. Einer anderen Generation wird sie in Fleisch & Blut übergegangen sein & sie wird die Wiederholungen langweilig finden. Für mich sind sie notwendig. – Diese Methode ist im Wesentlichen der Übergang von der Frage nach der Wahrheit zur Frage nach dem Sinn.

„(∃x):xⁿ + a₁xⁿ⁻¹ + … a_n = 0” Wenn ich das nicht extensiv auffasse, was sagt es? (Ein mathematischer Satz sagt immer das, was sein Beweis beweist. D.h. er sagt nie mehr, als sein Beweis beweist.)

Wenn ein Satz Sinn hat, muß auch sein Gegenteil Sinn haben.

Daß die Frage Sinn hat „wieviele Lösungen hat eine Gleichung” ist klar.
     [Die Antwort ist übrigens eine Zahlangabe, die man für ein Beispiel eines mathematischen Satzes höherer Type halten könnte; aber hier zeigt sich gerade, daß es das nicht gibt]

Der Satz „(x) x² + 2xy + y² = (x + y)²” ist hat Sinn & ist wahr, der Satz (x) x² = 2x hat Sinn & ist falsch. (Wenn ich ihn sehe kann ich sagen: „so? das werden wir gleich sehen, ob das wahr ist, dazu braucht man nur …” & nun kontrolliere ich ihn.)
     Der Satz (∃x) x² = 2x hat Sinn & ist wahr. Was aber ist ein dem zweiten Fall entsprechender Satz mit „(∃x)” der Sinn hat & falsch ist?
     Etwa (∃x) x² = 2x ∙ x = 1?

Aber wie ist es denn: Im letzten Falle kann ich allerdings sagen: Wir werden gleich sehen ob das wahr ist. Aber im vorhergehenden scheint das gar nicht zu gehen. (Aber im letzten konnte ich ja statt „(∃x)” ebensogut „(x)” schreiben. Es geht wenn z.B. in „(∃)x” „x” nur reelle Zahlen bedeutet || umfaßt. Das würde aber sagen, daß „(∃x) x² = 2x” sinnlos ist, wenn „x” die uneingeschränkte Zahlform ist.
     Hätte ich eine Methode Gleichungen die eine Lösung haben von solchen zu scheiden die keine haben dann hätte mit Bezug auf diese Methode der Ausdruck „(∃x) x² = 2x” Sinn.

Ich kann fragen „welche Lösung hat die Gleichung x² = 2x”, aber ich kann nicht fragen „hat sie eine Lösung”. Denn, wie würde das aussehen, wenn sie keine Lösung hätte? (Nicht extensiv!) Erst wenn ich weiß was der Fall ist wenn ein Satz falsch ist, hat er einen Sinn. – Wenn nun aber jener andere Fall etwa der der Gleichung „(∃x) x² ‒ 2x ‒ x(x ‒ 2) = 0” wäre? Dann hätte der Satz (∃x) x² = 2x allerdings Sinn & sein Beweis wäre daß die Regeln es nicht gestatten die Seiten gegeneinander zu kürzen.

Was aber beweisen die Beweise daß jede Gleichung n^ten Grades eine Lösung hat? Welche Fragen beantwortet dieser Beweis? Ich kann ja nicht ins Blaue hineinfragen!

Auf die Frage „hat die Gleichung xⁿ + a₁ xⁿ⁻¹ … a_n = 0 eine Lösung || gibt es eine Lösung der Gleichung xⁿ + a₁xⁿ⁻¹ … a_n = 0 ?” kann man immer fragen „Im Gegensatz wozu?”.

Wenn jene Beweise tun, was sie vorgeben dann müssen sie die Gleichungen der Form xⁿ + a₁ xⁿ⁻¹ etc. auffassen als einen Teil eines größeren Systems in dem der Gegensatz des zu beweisenden Sinn hat.

5 × 25 = 625
Worin besteht hier das System, das mir die Kommensurabilität zeigt?

Doch wohl darin daß mir die Multiplikation zweier in dieser Form hingeschriebener Zahlen nach der Regel immer wieder eine Zahl liefert derselben Form || in derselben Form liefert & eine Regel für zwei Zahlzeichen dieser Form entscheidet ob sie dieselbe oder verschiedene Zahlen bezeichnen.

Man könnte diese Auffassung auch so charakterisieren: Es ist unmöglich Entdeckungen neuer || neuartiger Regeln zu machen, die von einer uns bekannten Form gelten. Sind es neue Regeln so ist es nicht die alte Form. Das Gebäude der Regeln muß vollständig sein, wenn wir überhaupt mit einem Begriff arbeiten wollen. – Man kann keine Entdeckungen in der Syntax machen. – Denn erst diese Gruppe von Regeln bestimmt den Sinn unserer Zeichen & jede Änderung (z.B. Ergänzung) der Regeln bedeutet eine Änderung des Sinnes.

Ebenso wie man die Merkmale eines Begriffes

Ein System ist eine Formenreihe & die Operationen die sukzessive ihre Glieder erzeugen, sind eben in den Regeln beschrieben.

Der Gegensatz zu „es ist notwendig daß p für alle Zahlen gilt” ist allerdings „es ist nicht notwendig, daß …” und nicht „es ist notwendig, daß nicht …”. Aber nun denkt man: wenn es nicht notwendig ist daß es für alle Zahlen gilt, so ist es doch möglich. Aber hier liegt der Fehler, denn man sieht nicht daß man in die extensive Auffassung geraten ist: Der Satz „es ist möglich – wenn auch nicht notwendig – daß p für alle Zahlen gilt” ist unsinnig. Denn „notwendig” & „alle” gehören in der Mathematik zusammen. (Solange man diese Ausdrucksweise nicht überhaupt durch eine weniger irreführende ersetzt.)

Was kann denn (x) x² ≠ ‒ 1 bedeuten? Es kann doch nicht sagen, daß sämtliche Quadrate ungleich ‒ 1 sind.

Kann es uns aber nicht eine Anleitung geben & sagen „wenn du auf ein Quadrat stößt so ist es nicht || nie gleich ‒ 1”?

Aber ist nicht eben das die Art & Weise wie die Variable (ich meine die allg. Konstante) mit den Zahlen in Zusammenhang steht?

Ist also x² ≠ ‒ 1 || x² ≠ ‒ a das Gegenstück zu einer Definition?
     In sofern, ja, als es eine Form verbietet. Aber ist dann die Schreibweise richtig?

Der Unterschied in den Auffassungen der Variablen tritt hervor wo eine Variable einer Zahl gleichgesetzt wird.

(x + y)² liefert x² + 2xy + y² aber x kann doch nie 1 liefern!

Dient die Variable in „x² = 2x ∙ x = 2” nur zur Verknüpfung? (Als ‚links’)”

Man könnte auch so fragen: Wie habe ich die Beschreibung „die Lösung der Gleichung x² = 2x” in mathem. Symbolen auszudrücken?
So?: ‒

a 2

± √

a² 4

‒ b [x² ‒ 2x + 0 = 0]

Meine Schwierigkeit ist die: Wenn ich im Gebiet der reellen, rationalen, oder ganzen Zahlen Gleichungen nach den Regeln löse so komme ich in gewissen Fällen auf scheinbaren Unsinn. Wenn das nun eintritt: Soll ich sagen, es ist damit bewiesen daß die ursprüngliche Gleichung unsinnig war? So daß ich also erst nach beendeter Anwendung der Regeln sehen könnte ob sie unsinnig war oder Sinn hatte?! Muß es nicht vielmehr so heißen: Das Resultat der scheinbar unsinnigen Gleichung zeigt doch etwas über die allgemeine Form & bringt sie mit || die verbotene Gleichung mit solchen die eine normale Lösung haben sehr wohl in Verbindung. Die Lösung zeigt doch immer die Distanz der abnormalen zur normalen Lösung. Wenn z.B. √‒1 herauskommt so weiß ich daß √‒1 + 1 schon eine normale Lösung || Wurzel wäre. Die Kontinuität, die Verbindung mit der normalen Lösung ist nicht abgebrochen. Würde das bedeuten, daß im Begriff der reellen Zahlen wie wir ihn durch unseren Symbolismus & seine Regeln darstellen der Begriff der imaginären bereits präsupponiert ist?
     Das käme etwa darauf hinaus von der

Man könnte sagen, „sie schneidet ihn um einen gewissen Betrag nicht” & würde dadurch die Kontinuität mit dem normalen Schnitt darstellen. „Sie schneidet ihn || „Sie verfehlt ihn um einen bestimmten Betrag”.

Ich kann aber auch so sagen: Da ich aus ‒ 1 nicht die Wurzel ziehen kann, so darf ich auf die Gleichung x² = ‒ 1 nicht die Regel anwenden, die mich sonst von x² = a zu x = √a bringt. Ich stocke also bei x² = ‒ 1.

Wenn ich also schreibe ~(∃x) x² + 2x + 2 = 0, so könnte das behaupten, daß ich bei der Auflösung der Gleichung zu einer Stockung kommen werde.

x² ‒ 3x ‒ x(x ‒ 3) = 0 x² ‒ 3x ‒ 2 = 0

Die linke Seite ist wirklich = 0 Hier ist ¤ sie's nicht.

x² + 3x + 2 = 0 x = ‒ 1

}

Das ist wieder wie ein allgemeiner Satz & hier ist die Variable ein Glied. Denn schließlich könnte ich ja auch so schreiben: { ‒ 1}² + 3{ ‒ 1} + 2 = 0. Und hier könnten die geschweiften Klammern offenbar alles andeuten was oben die Variable ausgedrückt hat.

Kann man die Vorhersage daß die Gleichung nicht zu einer Stockung führt durch Gleichungen ausdrücken?

5 ˃ 4 sagt || heißt die Gleichung 4 + x = 5 führt zu keiner Stockung. Wenn ich nun frage „ja wie kann ich es denn wissen, wenn etwas eine Stockung ist” so müßte man mir ein allgemeines Kriterium geben, das mir in jedem speziellen Fall entscheiden hilft, ob ich weiter operieren kann (die Regeln geben diese Kriterien). So ein Kriterium in einem besonderen Fall wäre es, zu sagen, „es darf nicht das Zeichen √ ‒ 1 gebildet werden, du mußt vor diesem Zeichen halt machen”.
     Wie aber kann ich das allgemeine Kriterium dafür geben daß ich die größere Zahl nicht von der kleineren abziehen darf? Das geht doch selbstverständlich nur mit Hilfe von Variablen. (Mit Rekursion) Es heißt dann „eine Zahl ist immer größer als eine andere wenn sie so & so aussieht”; oder „wenn die Differenz so & so aussieht dann mache halt.” Dieses „so & so” muß aber mit Hilfe der Variablen beschrieben werden. Und was ist das nun für eine Variable? Vor allem ist eines wesentlich; die Gleichung oder Ungleichung in der sie vorkommt kann nicht eine sein die man beweisen kann. Denn die Variable darf sich nicht wegheben, sonst könnte ich die Regel nicht im besondern Fall anwenden. Sie entspricht der Definition die auch eine Variable derselben Art enthält. x ∙ x = x² Def. Das kann man nun wirklich als die Vorschrift auffassen für alle Ausdrücke „x ∙ x” die einem unterkommen den entsprechenden Ausdruck „x²” zu setzen. Hier ist die unendliche Möglichkeit im Endlichen fixiert. In der Definition deute ich nur die unendliche Möglichkeit an. [ 1 + 1 = 2 Def. hier dasselbe wie oben]

Das „(∃x)” bezieht sich immer auf die Ausrechnung einer Gleichung & auf das was dabei herauskommen soll.

Wie ist es mit dem Satz: „die Gleichung x² + 3x + 2 = 0 ergibt eine Quadratzahl als Lösung”? (oder eine gerade Zahl etc. etc.)